Soy un usuario impenitente de la hoja de cálculo. Comencé con la vetusta Visicalc, pasé a la vieja (que no obsoleta) Lotus 1-2-3, con la que hice muchos cálculos para mi tesis doctoral, y ahora mezclo la Excel de Windows con la LibreOffice Calc para todo tipo de cálculos. Me resulta particularmente útil como base de datos, pero en mi opinión tiene un gran valor para el cálculo científico. No está mal para haber sido diseñada en sus inicios como herramienta de cálculo financiero.
Por supuesto, para cálculos gordos nada me va mejor que el lenguaje Fortran, pero no es algo que no todo el mundo maneja, y los programas o aplicaciones en boga hoy día pueden estar descatalogadas en diez años y convertidas en historia antigua en veinte. Soy perro viejo en este asunto, así que sé de lo que digo. Sin embargo, el funcionamiento de una hoja de cálculo apenas ha cambiado, y de todas las herramientas informáticas que he usado es una de las que mejor ha perdurado.
Por ambos motivos (utilidad y perdurabilidad) me he decidido a abrir esta sección de Física con Excel. Plantearé algunos problemas físicos y los resolveremos. Os incluiré copia de la hoja completa al final del post para que podáis jugar con ella. Espero que os será útil, y por supuesto podéis colaborar con vuestras propias ideas y sugerencias.
ADVERTENCIAS. No prejuzgo las cualidades de la hoja Excel (Windows) con la Calc (LibrreOffice, OpenOffice) o ninguna otra. Me limito a usarla y mencionarla aquí porque más personas están familiarizadas con ella. Utilizaré la versión de 2003 porque estoy harto de tener que cambiar cada vez que al señor Microsoft le da por ahí. Eso significa que debéis tener cuidado porque algunas funciones cambian de nombre con cada nueva versión. Finalmente, supondré que tenéis algunos conocimientos del uso de una hoja de cálculo, no necesariamente profundos sino lo bastante para moveros con cierta comodidad.
Y ahora que estáis convenientemente advertidos, comencemos. Voy a inaugura esta sección con el llamado problema del camino del borracho. A pesar de su nombre poco serio representa multitud de procesos como, por citar uno, el movimiento browniano. Se trata de lo siguiente. Supongamos que tenemos un borracho que quiere ir a su casa. Como no da pie con bola, cada paso que da le lleva a una dirección distinta, aunque para simplificar supondremos que todos los pasos tienen la misma longitud, digamos L. Es decir, se trata de simular el comportamiento de un objeto que se mueve a pasos discretos, con longitud constante y dirección aleatoria.
Digamos que en el paso cero el borracho se encuentra en la posición (x0,y0). Para el paso 1, de longitud L, tomamos un valor aleatorio de la dirección que va a seguir, y que podemos caracterizar por el ángulo α1. Eso nos da las coordenadas cartesianas de la nueva posición:
x1=x0+L*cos(α1)
y1=y0+L*sen(α1)
A continuación hacemos lo mismo con el paso 2, es decir, nuevo ángulo aleatorio y nueva posición:
x2=x1+L*cos(α2)
y2=y1+L*sen(α2)
y así sucesivamente:
xi=xi-1+L*cos(αi)
yi=yi-1+L*sen(αi)
Al cabo de N pasos la posición del borracho vendrá dada por las coordenadas (xn,yn), que podemos escribir de esta forma:
 Por supuesto, tanto al final como en cada paso podemos obtener la distancia al origen:
Por supuesto, tanto al final como en cada paso podemos obtener la distancia al origen:
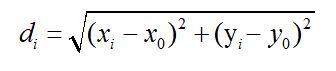 Podríamos comenzar, pero siempre que haya posibilidad de simplificar, se simplifica. La idea es hacer que el borracho parta del origen de coordenadas. Si resulta que ya está allí, es decir, que (x0,y0)=(0,0), tanto mejor, pero si no es el caso no tenemos más que hacer un cambio de variable y definir x’=x-x0, y´=y-y0. Con ello hemos llevado nuestro objeto al origen de coordenadas.
Podríamos comenzar, pero siempre que haya posibilidad de simplificar, se simplifica. La idea es hacer que el borracho parta del origen de coordenadas. Si resulta que ya está allí, es decir, que (x0,y0)=(0,0), tanto mejor, pero si no es el caso no tenemos más que hacer un cambio de variable y definir x’=x-x0, y´=y-y0. Con ello hemos llevado nuestro objeto al origen de coordenadas.
Hora de trabajar. Abramos una hoja de cálculo vacía y comencemos. Lo primero que haremos es definir nuestra variable L, la longitud del paso. Voy a introducirla en la casilla C3 de la hoja de cálculo. ¿Por qué en esa casilla precisamente? Pues por ningún motivo en especial, salvo porque me resulta cómodo.
A continuación voy a usar las columnas A, B, C, D, E, que respectivamente serán el número de paso (N), el ángulo α, la coordenada x, la coordenada y, y la distancia d. Comenzaré por la fila 9, donde pondré los datos correspondientes a N=0. En ese caso, será todo cero.
Pasamos a la siguiente fila, la 10. La casilla A10 será el siguiente valor de N, pero en lugar de introducir el valor uno haré que sea igual a la casilla anterior mas una unidad, esto es A10=A9+1. Luego explicaré por qué. La casilla B10 será el ángulo α1. Es aleatoria así que usaré la función ALEATORIO() de la hoja de cálculo. Esa función nos da un número al azar entre 0 y 1. Necesitamos un ángulo, y como las funciones trigonométricas de la hoja se expresan en radianes, ese ángulo variará entre 0 y 2π. Nada más fácil: B10=2*PI()*ALEATORIO()
Siguiente fila. C10 será x1, y eso será igual a x0+L*cos(α1), como vimos antes, de modo que hagamos C10=C9+$C$3*COS(B10). De modo similar la casilla D10 será la componente y1, lo que se consigue haciendo D10=D9+$C$3*SENO(B10). En ambos casos, la casilla C3 es, os recuerdo, donde está el valor de L. Y la casilla E9, que nos dará la distancia recorrida será la raíz de la suma de cuadrados de las coordenadas, es decir, E10=RAIZ(C10*C10+D10*D10).
Quizá os estéis preguntando ¿Por qué he puesto $C$3 en lugar de C3? Porque si no el siguiente paso no funciona. Ese paso es, sencillamente, copiar fórmulas de las casillas A10 a E10 y pegarlas en la siguiente fila (A11 a E11). Resulta que, cuando relacionamos una casilla con otras, esas relaciones son relativas. Por ejemplo, si hacemos algo del tipo C10=C9+C3 la hoja lo interpreta como “casilla actual (C10) igual a la casilla inmediata superior (esa es C9) mas la que se encuentra siete posiciones por encima de la casilla actual (esa es C3)” Si copias la casilla C10 en la casilla C11, ésta queda como C11=C10+C4. Si eso es lo que quieres, bien, pero ¿y si lo que quieres hacer es que cada casilla sea igual a la inmediata superior mas lo que haya en C3?
Para esos casos es cuando sirven los símbolos esos del dólar. Hacer C10=C9+$C$3 se traduce como “casilla C10 igual a la casilla inmediata superior (esa es C9) mas la casilla C3, y siempre la C3”. De ese modo, al copiar y pegar en la casilla inferior saldría C11=C10+$C$3, donde esa $c$3 siempre será la casilla de la tercera fila y tercera columna. En otros casos podemos fijar solamente la fila o la columna, pero eso ya lo veremos en su momento.
De acuerdo, pues ya que tenemos la fila 10 (para N=1) y la fila 11 (para N=2) no hay más que copiar y pegar todas las filas que nos de la gana. Yo lo he hecho hasta N=1000. Fijaos que cada vez que hagáis una modificación a la hoja, o incluso si la guardáis, los valores de las columnas C, D y E cambian. Eso es porque la función ALEATORIO() cambia de valores a cada ocasión.
Ya falta poco, salvo hacer una bonita gráfica. He hecho dos gráficas. Una de ellas es una gráfica X-Y que muestra las posiciones por donde ha estado el borracho, como si lo hubiésemos seguido con un dron.
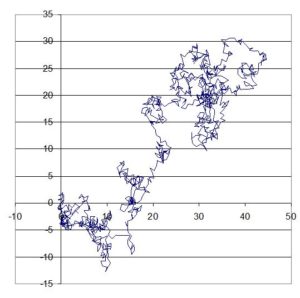 En este caso nuestro borracho terminó en las coordenadas (x,y)=(23.69, 21.08), a una distancia d=33,12L. Si hubiese caminado en línea recta hacia la derecha habría llegado a 1000L veces, así que como podemos ver le queda todavía un buen trecho. En general, la distancia promedio teórica a que el borracho suele llegar tras N pasos es igual a la raíz cuadrada de N.
En este caso nuestro borracho terminó en las coordenadas (x,y)=(23.69, 21.08), a una distancia d=33,12L. Si hubiese caminado en línea recta hacia la derecha habría llegado a 1000L veces, así que como podemos ver le queda todavía un buen trecho. En general, la distancia promedio teórica a que el borracho suele llegar tras N pasos es igual a la raíz cuadrada de N.
Podemos verlo en la segunda gráfica, la típica de líneas donde se muestra la distancia de cada paso. La línea gruesa es el valor teórico al que tiende la distancia, que es igual a la raíz cuadrada de N:
 En este caso los valores para N=1000 coinciden bastante bien, pero no sucede lo mismo para otros valores de N, ni tampoco para otras gráficas. Esta es una modificación de la hoja para diez simulaciones:
En este caso los valores para N=1000 coinciden bastante bien, pero no sucede lo mismo para otros valores de N, ni tampoco para otras gráficas. Esta es una modificación de la hoja para diez simulaciones:
 Lo divertido es que, como he dicho, la variación de la variable ALEATORIO() hace que cada vez que toquéis algo en la hoja, o la guardéis, la gráfica sea distinta. Podéis jugar con la hoja Excel, que os incluyo al final de este post. Jugad con ella lo que queráis, y modificadla a placer. Hay muchas opciones que no hemos explorado. Por ejemplo: ¿y si la longitud L del paso también varía aleatoriamente? ¿Y si el borracho solamente tiende a moverse en direcciones hacia la mitad derecha en lugar de en cualquier dirección? En una versión alternativa, llamada “camino del marinero borracho”, los movimientos solamente pueden ser en vertical u horizontal. ¿Y si…? Pues a jugar se ha dicho. Espero vuestros comentarios. Sobrios, por favor.
Lo divertido es que, como he dicho, la variación de la variable ALEATORIO() hace que cada vez que toquéis algo en la hoja, o la guardéis, la gráfica sea distinta. Podéis jugar con la hoja Excel, que os incluyo al final de este post. Jugad con ella lo que queráis, y modificadla a placer. Hay muchas opciones que no hemos explorado. Por ejemplo: ¿y si la longitud L del paso también varía aleatoriamente? ¿Y si el borracho solamente tiende a moverse en direcciones hacia la mitad derecha en lugar de en cualquier dirección? En una versión alternativa, llamada “camino del marinero borracho”, los movimientos solamente pueden ser en vertical u horizontal. ¿Y si…? Pues a jugar se ha dicho. Espero vuestros comentarios. Sobrios, por favor.
[Hoja de cálculo disponible: el camino del borracho]


Buenas tardes
a pesar de usar EXCEL y Numbers (mac) de forma intensiva nunca pense en su uso para simular el movimiento browniano
Se me ocurre la segunda derivada trasladar la sistemática a Mat Lab usando una dinámica de montecarlo para digamos un millon de vectores … el resultado puede ser expectacular
buen articulo, pero al ir a ver la pagina excel y pinchar en ella, me dice que dicha pagina no existe, puedes solucionarlo
Hola, acabo de comprobarlo y sí está en su sitio. Comprueba otra vez, y si sigues sin conseguirlo avísame. AQ
A mi tampoco me funciona el enlace pero como explicas como hacerlo paso a paso tampoco es tan importante. Es mas, casi prefiero implementarlo en C o en Matlab 😉
En cuanto al articulo y la seccion, me parece interesantisimo, muchas gracias! Espero que sigas poniendo mas articulos, tengo la idea de que se pueden hacer muchas cosas con excel pero no se muy bien que. Ademas que no lo uso mucho en el dia a dia.
Gracias por el artículo.
Comentar que funciona también el LibreOffice Calc con la peculiaridad de que si bien mucha gente tiene Excel pero porque roban (pues cuesta mínimo 100 euros la versión de estudiante y mucho más la estándar y la profesional) y son a su vez robados al comprar un portátil donde les obligan a comprar MS Windows que cuesta más de 90 euros en su versión más barata (Home Basic OEM) aunque luego lo desinstalen para instalar un potente y gratuito GNU/Linux.
Es interesante el comportamiento de las funciones ALEATORIO que sí son diferentes en Excel (donde cambian a cada modificación en la hoja) y LibreOffice Calc (solamente cambian al pulsar CTRL+MAY+F9 o al volver a abrir el fichero). Con el comportamiento de una y otra se pueden realizar distintos juegos, les dejo un Master Mind que solo funciona en principio en Calc: https://esperanto.us.es/index.php/component/jdownloads/summary/4-mastermind