Me he resistido hasta ahora a hacer simulaciones sobre la epidemia de coronavirus que nos rodea. Ya hay demasiados estadísticos de salón intentando predecir una pandemia con un simple SRI. Yo no voy a hacerlo, aunque una vez jugué con un modelo para el apocalipsis zombi.
Sin embargo, hace unas horas publiqué unos datos sobre la evolución de la epidemia y las respuestas recibidas me hacen pensar que puede interesaros en general, así que voy a aprovechar para ilustrar algunos conceptos físico-matemáticos.
En ciencia estamos acostumbrados al concepto de ajuste. Imaginad que tenemos dos columnas de datos, en cada una de las cuales hay una pareja (x,y) de datos estilo “variable independiente – función”. Por ejemplo, estiramos un muelle una cantidad x1, y el muelle hace una fuerza recuperadora F1; otro estiramiento x2, otra fuerza F2. Así tenemos un conjunto de datos: (x1,F1), (x2,F2)… (xn,Fn).
Hagamos una gráfica donde el eje horizontal contiene los datos de x, y el eje vertical los datos de F (lo que se llama “F en función de x”). En un mundo ideal donde manda la ley de Hooke los puntos experimentales forman una recta perfecta; pero como siempre hay errores (materiales, ambientales, humanos) los puntos se desviarán de dicha recta. Se trata entonces de hallar la recta de mejor ajuste; es decir, aquella recta cuya distancia a los puntos experimentales es la menor posible. Es una de las cosas que siempre explico a mis alumnos en clase de prácticas.
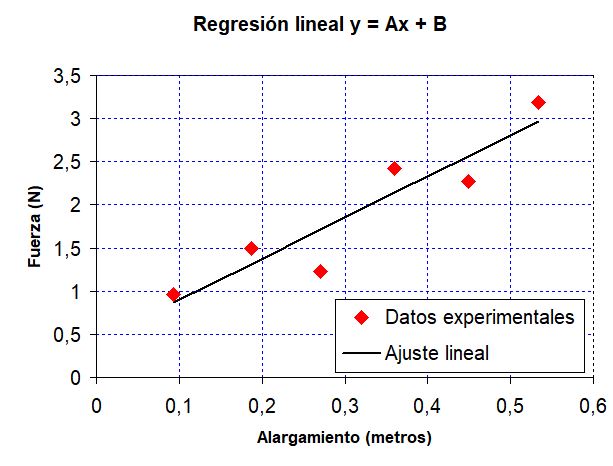
La siguiente imagen es un ejemplo con datos experimentales de unos alumnos míos del curso pasado que he retocado levemente para meterle algo más de “ruido”. Para el ajuste he usado una hoja de cálculo que tengo configurada para ellos (y que podéis usar libremente descargándola aquí).
No es que los puntos ajusten muy bien, al menos en apariencia (los he estropeado deliberadamente para realzar el efecto), pero aun así, parece que se comportan más o menos como una recta.
Hay tres datos importantes en un ajuste lineal. Dos de ellos son la pendiente (A) y la ordenada en el origen (B), que nos da la ecuación de la recta continua: y=Ax+B (en nuestro caso y es la fuerza y x el alargamiento); el tercer dato es el llamado coeficiente de regresión r, que nos dice hasta qué punto esos datos forma a una recta.
Para esa gráfica sale una pendiente A=4,78 (que, en nuestro caso, nos da la constante elástica del muelle), una ordenada en el origen B=0,42 (en teoría debería ser cero, pero aquí hay un error del orden de 0,3 así que no va mal del todo). En cuanto a r, sale un valor de 0,93, un valor decente para este caso.
Antes de seguir, un pequeño detalle. La hoja que os comenté antes (hela, que diría Forges) calcula la recta de ajuste a las duras, es decir, haciendo multiplicaciones y sumas. En Excel hay funciones ya hechas para este ajuste: PENDIENTE(), INTERSECCION.EJE() y COEF.DE.CORREL(). He usado estas funciones en la Excel que os adjunto al final de este artículo por comodidad.
¿Qué pasa cuando los puntos no forman una recta sino otro tipo de curva? Pues en muchos casos podemos cambiar las variables para convertirlos en rectas. Por ejemplo, la relación entre el período T de un péndulo y la longitud L del hilo es esta: T=2π(L/g)1/2, donde g es la aceleración de la gravedad. Si hacemos una gráfica “T en función de L” (es decir, T va en el eje vertical y L en el horizontal) está claro que no nos saldrá una recta porque T varía con la raíz cuadrada de L. Pues aquí va el truco del almendruco: si graficamos T en función de L1/2, entonces sí tenemos una recta.
Es lo que sucede con las gráficas del coronavirus. Durante cierta fase de una epidemia los casos aumentan exponencialmente con el tiempo. Eso quiere decir que el número de casos se puede escribir como N(t)=No*exp(t/τ), donde “exp” es la función exponencial, No es el número de casos para t=0, y τ es un parámetro que nos mide lo rápido que aumenta la función. La tasa de duplicación Td= τ/Ln(2) nos da el tiempo que ha de pasar para que el número de casos se multiplique por dos.
Para hacer un ajuste lineal tomamos logaritmos en la ecuación de N(t), con lo que obtenemos Ln(N) = Ln(No) + t/τ. Eso significa que, si hacemos un ajuste lineal tomando el tiempo como variable x y Ln(N) como variable y, la pendiente de la recta nos dará la cantidad 1/τ. O de otro modo, la pendiente multiplicada por Ln(2) nos dará la tasa de duplicación.
Vamos al ajuste. He tomado los datos del Instituto de Salud Carlos III (covid19.isciii.es) para la tasa de fallecimientos y para el número total de casos detectados. Mi momento inicial (t=0) es el día 15 de marzo, es decir, el inicio del Estado de Alarma. Lo he hecho así porque he visto que en días anteriores la curva es otro tipo de exponencial (indudablemente la situación era distinta antes del confinamiento).
Escribo estas líneas el día 26, por lo que tengo datos hasta el día 25 inclusive. Este es el resultado:
El ajuste se verá mucho mejor si el eje vertical lo ponemos en una escala logarítmica:
Como véis el ajuste no es perfecto, pero se aproxima bastante a una exponencial. Los datos a día de hoy son:
CASOS TOTALES: r=0,987 Tasa de duplicación: 3,87 días
FALLECIMIENTOS: r=0,964 Tasa de duplicación: 2,74 días
A día de hoy jueves hay un total de 56.188 casos y 4.089 fallecimientos. De seguir la tendencia marcada por el ajuste, el próximo domingo los casos ascenderán a 118.000 y los fallecimientos a 9.420. Pero eso de “seguir la tendencia” no está asegurado, porque es como decir que mi sobrino, si sigue creciendo como hasta ahora, medirá diez metros para el 2025. Es lo que tiene la función exponencial, que crece brutalmente sin limitación.
Ahora viene la buena noticia: esto no puede seguir así eternamente. Con el tiempo la exponencial se irá atenuando y se convertirá en algo parecido a una función logística). Estoy deseando poder ajustarla, porque eso significará que ya hemos pasado el punto de inflexión y los casos irán aumentando cada vez más lentamente. Cruzad los dedos. Y quedaos en casa.
NOTA FINAL. Estrictamente hablando, hoy puede que hayamos alcanzado el punto de inflexión para el número de fallecimientos, ya que ha descendido respecto al día anterior (25/3: +654 frente a 24/3:+738). Esto puede ser simplemente ruido estadístico, es decir, no conforma una tendencia clara. Hay que esperar.
[Hoja de cálculo disponible: Ajuste exponencial y coronavirus]